牛顿法
这个在线计算器实现了牛顿方法(也称为牛顿-拉弗森方法),用于寻找实数值函数的根(或零)。
它使用 导数计算器 实现牛顿法,以获得一个给定函数的导数的分析形式,因为这个方法需要它。你可以在计算器下面找到一个理论来回忆方法的基本知识。
牛顿-拉弗森方法1
在数值分析中,以牛顿和拉普森命名的牛顿方法(也称为牛顿-拉普森方法)是一种寻找实数值函数的根(或零)的连续较好近似值的方法。
该方法从定义在实数x上的函数f、该函数的导数f′和函数f的一个根的初始猜测x0开始。如果该函数满足公式推导中的假设,并且初始猜测很接近,那么更好的近似值x1就是
几何上, (x1, 0)是x轴和f的图形的切线在(x0, f(x0))的交点。
当 时,该过程重复, 直到达到一个足够准确的值。
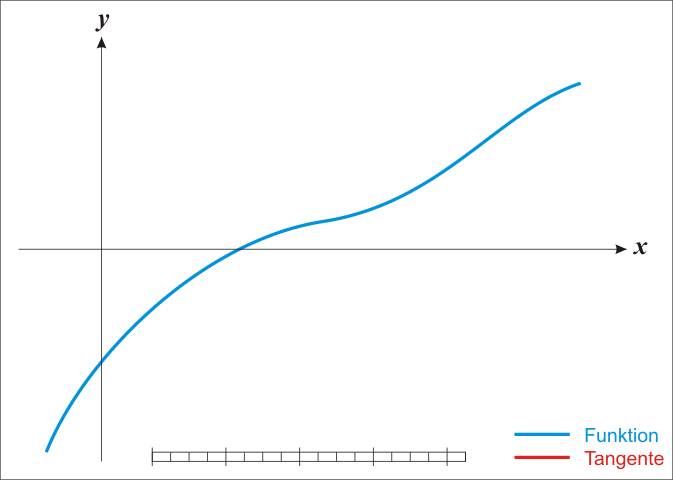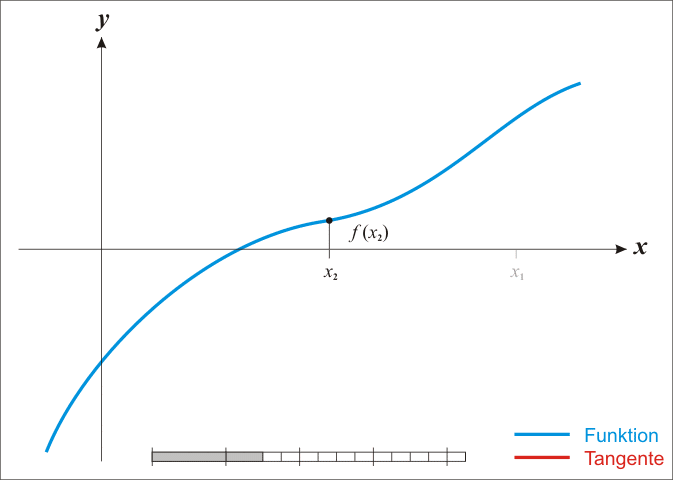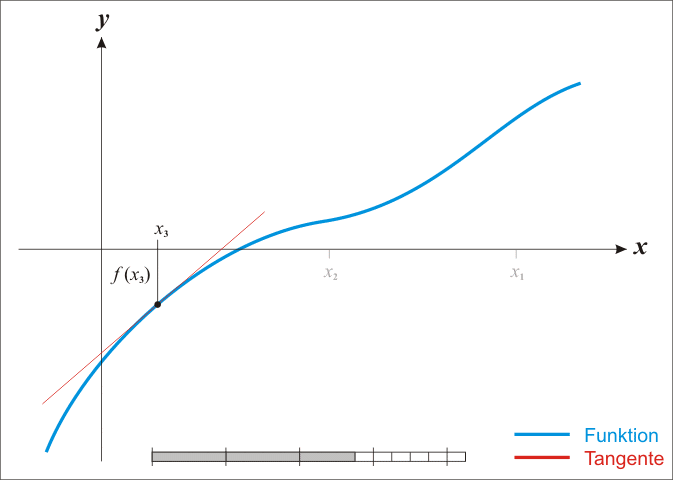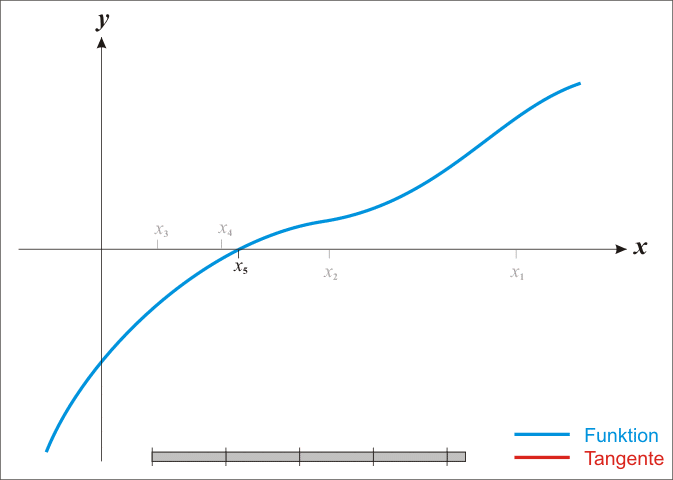
该方法的思路如下:从一个合理地接近真实根的初始猜测开始,然后用其切线来近似函数(可以用微积分的工具来计算),并计算该切线的x轴截距(用初级代数很容易做到)。这个x轴截距点通常比原来的猜测更接近于函数的根,而且这个方法可以反复进行。
牛顿法是一种非常强大的技术——通常收敛是二次的:当方法收敛于根时,根和近似值之间的差异在每一步都进行平方(准确数字的数量大约加倍)。 但是,该方法存在一些难点:计算函数的导数有困难,如果不满足牛顿方法二次收敛的假设,该方法就不能收敛到根上,对于倍数大于1的根,收敛速度很慢。
URL 复制到剪贴板
类似计算器
- • 割线法
- • 用洛必达法则解极限问题
- • 牛顿多项式插值
- • 定点迭代法
- • 模运算
- • 代数 部分 ( 24 计算器 )
PLANETCALC, 牛顿法
评论