螺旋物计算器
这个在线计算器从已知的维度计算未知的阿基米德螺旋维度。螺旋尺寸包括:外径、内径、分离距离(臂距、厚度)、螺旋长度、圈数
这是计算阿基米德螺旋的通用计算器。

我们有五个螺旋尺寸:外径—D,内径—D,厚度、分离距离或臂距— t,螺旋长度—L,圈数— n。这些尺寸相互关联(见下面的公式计算器),如果你知道任意三个参数,就可以计算其它两个参数。
生活中我们可以在卷起的物体中看到螺旋:卷纸、磁带、胶片等等。 你可以很容易地找到这些物体的尺寸,比如直径和厚度,或者圈数,然后用下面的计算器,计算出未知的尺寸量。 例如,你可以从卷的内径和外径,厚度或卷数计算出卷的长度。 当你知道圏的长度时,也可以解决一个相反的问题,即使用卷长度和内外径计算厚度和卷数。 像往常一样,理论和公式都可以在计算器下面找到。
当您输入已知的尺寸时,请小心单位控制!20米和20毫米不一样...
阿基米德螺旋
阿基米德螺旋(也称为算术螺线)是一个螺旋线,对应于一个点M以恒定的速度,沿着直线OA离开中心点O运动,同时OA以恒定的角速度围绕中心点O旋转时产生的轨迹。

如果我们把O到M的距离表示为 ρ,旋转角度表示为 φ,那么我们可以用极坐标方程来描述螺旋:
,
其中 k 是尺寸参数, 等于当角度旋转1弧度时距离的变化。 每转一圈(角度增加 2π ), 距离增加 2πk 。
这种增加是一个螺线两个臂之间的距离,分离距离,或螺旋厚度。我们可以用 a 重写初始方程:
由于厚度是恒定的,M点离中心越远,螺旋越像圆。
为了推导螺旋长度的公式,我们将研究无限小长度的变化。
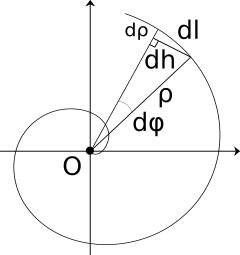
一个无限小的螺旋线段 dl 可以被认为是三角形 dl 、dρ 和 dh 的斜边。因此:
一个无限小的螺旋段 dh 可以用一个半径为 ρ 的圆的无限小段代替; 因此它的长度是ρdφ 。
利用螺旋的极坐标方程,我们可以用 kφ 代替 ρ,用 kdφ 代替 dρ
现在我们有长度 dl 和角度 dφ 的关系。为了求出长度,我们需要从起始角度到终点角度进行积分。
长话短说,最终积分是:
如果螺旋从零度开始(从中心开始),公式就简化成:
但在现实中,一卷材料当然不是从中心开始的。通常它有一个套管,因此有内径和初始角度。这些参数是如何关联的?
下面是圈数 n 与角度的关系:
这就是直径与角度的关系(这直接来自于螺线极坐标方程)
这些都是我们需要用已知尺寸来求未知尺寸的公式。 但请注意,长度方程是超越方程,而相反的任务(长度是已知的,求其它未知尺寸)需要数值方法。 这个计算器使用正割法。
评论