Regula Falsi Verfahren
Das Regula Falsi Verfahren ist ein Algorithmus zur Wurzelfindung, der eine Folge von Wurzeln von den Sekanten mit der Bisektionsmethode verwendet, um eine Wurzel von einer Funktion f zu approximieren.
这个页面的存在是由于以下各位的努力:
 | Timur
|
Stefan Roesner
|
本内容采用知识共享署名/相同方式共享许可协议3.0（未移植）进行许可。这意味着你可以在相同的许可条件下自由地重新发布或修改本内容，并且必须在你的网站上放置一个超链接到本作品https://zh.planetcalc.com/3712/，以注明原作者。此外，请不要修改本内容中对原作的任何引用（如果有的话）。
Eine Beschreibung des Regula Falsi Verfahren kann man unter dem Rechner finden.
Regula Falsi Verfahren
Regula Falsi Verfahren
Das Regula Falsi Verfahren ist ein Algorithmus zur Wurzelfindung, der die Eigenschaften der Bisektionsverfahren Sekanten-Verfahren kombiniert.
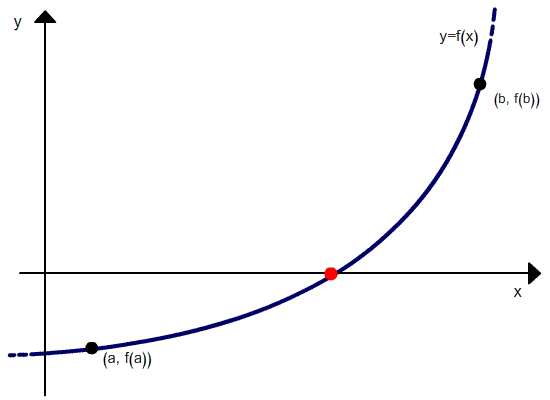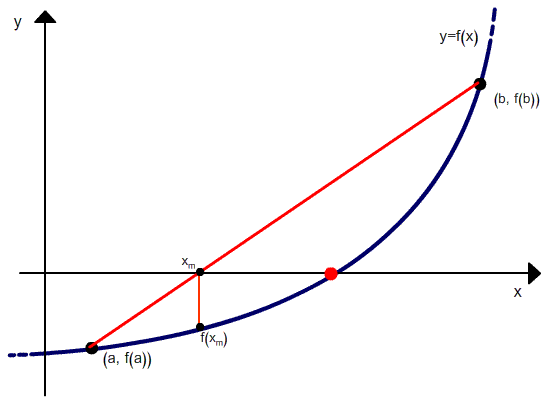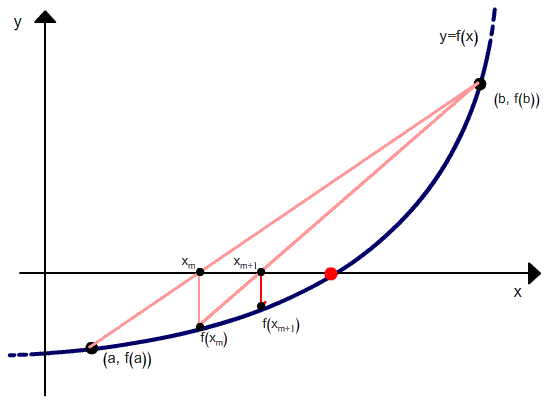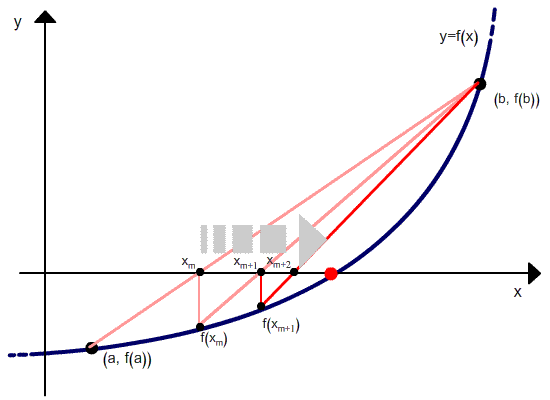
Wie im Sekanten-Verfahren nutzt man die Wurzel einer Sekanten (der Wert von X wie y=0) um die nächste Wurzelapproximation für die Funktion F zu berechnen.
Die Ableitung von der Rekursionsrelation ist die gleiche wie bei dem Sekanten-Verfahren:
Nimmt man mal an, dass man die Anfangswerte xO und x1 mit den Funktionswerten f(x0) and f(x1) hat.
Die Sekante hat die Gleichung
Daher ist die Wurzel der Sekante (wobei y=0)
Die obige Formel wird ebenfalls im Sekanten-Verfahren genutzt, aber das Sekantenverfahren behält immer die letzten beiden berechneten Punkte, während im Regula Falsi Verfahren immer zwei Punkte beibehält, die immer eine Wurzel einklammern.
Eine graphische Interpretation kann man unten sehen.
Quelle
Wie man an der Rekursionsrelation sehen kann, benötigt das Regula Falsi Verfahren zwei Anfangswerte, x0 und x1, welche die Wurzel einklammern sollten. Aber im Gegensatz zum Bisektionsverfahren geht die Breite der Klammern bei den Iterationen nicht gegen Null.
Die Toleranzbedingung kann einer der zwei Möglichkeiten sein:
— Funktionswert ist geringer als ε.
— Differenz zwischen zwei aufeinanderfolgenden xk ist geringer als ε. Bitte beachten, dass die Differenz zwischen den zwei berechneten aufeinanderfolgenden xk, und nicht der Endpunkte des Intervalls.
Mehr zum Thema: Regula Falsi Verfahren
评论