在线计算器: Volumen eines geneigten zylindrischen Tanks

Um die Berechnung für diesen Rechner durchzuführen, muss man die Tankgröße, Winkel und Füllstand angeben.

Messung des Füllstandes

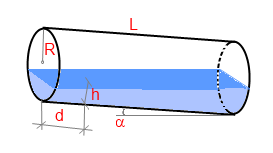
Man muss den Füllstand an der Mittellinie des Tanks senkrecht zum Tankboden messen (siehe Bild). Man kann den Füllstand an jeder Distanz von einer der Basen messen (wenn man dies macht, muss man die Distanz als speziellen Parameter eingeben).
Alternativ kann man den Tank so neigen, sodass der Null-Füllstand an der obersten Basis liegt; in diesem Fall muss man nur den Neigungswinkel messen.

Man kann die Details der Berechnung und die Formeln unter dem Rechner finden.

Flüssigkeitsvolumen in einem geneigten zylindrischen Tanks

Zylinderlänge

Radius des Zylinders

Neigungswinkel (Grade)

Füllstand

Flüssigkeitsstand gemessen in der Nähe von

Obere Basis

Untere Basis

Distanz zur Basis

Distanz zwischen der Messstelle des Flüssigkeitsstand und der nächsten Basis (0 wenn der Füllstand direkt in der Nähe der Basis gemessen wird)

Präzesionsberechnung

Zahlen nach dem Dezimalpunkt: 2

Flüssigkeitsstand in der Nähe der oberen Basis

Flüssigkeitsstand in der Nähe der unteren Basis

Länge des teilweis gefüllten Teils des Tanks

Länge des vollgefüllten Teils des Tanks

Flüssigkeitsvolumen

Ich konnte keine fertige Lösung zur Berechnung der Flüssigkeit Volumen in einem geneigten Zylinder finden, daher habe ich die Formel folgendermaßen abgeleitet:

Formel für das Volumen eines teilgefüllten geneigten Tanks

$V = \frac{R^2}{2}\int_{\small0}^L {\theta(x)-\sin{\theta(x)}dx$
wobei $\theta(x)$ - zeigt, wie der Segmentwinkel von der Zylinderlänge x abhängt.
Dies kann wie folgt abgeleitet werden:
$\theta(x)=2\arccos{\frac{R-h}{R}}=2\arccos{\frac{R-(x\tan{\alpha}+h_{0})}{R}}$
wobei
a - Neigungswinkel,
h0 – Füllstand an der oberen Basis ist

Wenn man diese Darstellung der Formel substituiert, erhält man:
$V = R^2\int_{\small0}^L {\arccos{u}-u\sqrt{1-u^2}dx=-\frac{R^3}{\tan{\alpha}}\int_{\small{u_0}}^{u_L} {\arccos{u}-u\sqrt{1-u^2}du$
wobei $u=\frac{R-(x\tan{\alpha}+h_{0})}{R}$ ist.

Wenn man das Integral nimmt, erhält man:
$V = -\frac{R^3}{\tan{\alpha}}\left( u\arccos{u}-\frac{1}{3}\sqrt{1-u^2}(u^2+2)\right)\large|_{\small{u_0}}^{u_L}$
$= \frac{R^3}{\tan{\alpha}}\left( K\arccos{K}-\frac{1}{3}\sqrt{1-K^2}(K^2+2)-{C}\arccos{C}+\frac{1}{3}\sqrt{1-C^2}\left(C^2+2\right) \right)$

wobei
$K=1-\frac{h_{0}}{R}$ ,
$C=K-\frac{{L}tan{\alpha}}{R}$ ist.

Gefüllter Teil der Tanklänge bestimmen

Die obige Formel wird für die Berechnung des Volums eines geneigten Tanks mit den folgenden Annahmen verwendet:

Beide Basen sind teilweise mit Flüssigkeit gefüllt.
Der Füllstand h₀ wird direkt an der oberen Basis gemessen.
Kein Teil des Tanks ist leer oder komplett gefüllt.

Aber der Rechner erlaubt auch den Füllstand in einer Distanz in der Nähe von der oberen oder unteren Basis. Ein Teil des Tanks kann dann auch komplett gefüllt sein.

Um den Füllstand direkt an der oberen Basis h_u zu berechnen, nutzt man die Formel:
$h_u=h_{ll}-(L_c-l_l){\tan{\alpha}}$
wobei h_ll - der Füllstand zur Distanz l_l von der unteren Basis und L_c - die Länge des Tanks ist.
$h_u=h_{lu}-l_u{\tan{\alpha}}$
wobei h_lu - der Füllstand gemessen zur Distanz l_u von der oberen Basis.
Falls die h_u gleich oder über Null ist, nimmt man an, dass h₀=h_u, und L_f = L_c ist.

Leerer Teil des Tanks

Die h_u kann auch negative sein. Das bedeutet, dass ein Teil des Tanks leer ist. In diesem Fall nimmt man an, dass die h₀=0 ist und man berechnet den übrigen (gefüllten) Teil L_f mit der folgenden Formel:
$L_f=L_c+\frac{h_u}{\tan{\alpha}}$
wobei L_c die Zylinderlänge ist.

Voll gefüllter Tank

Der Füllstand direkt an der unteren Basis h₁ kann folgendermaßen bestimmt werden:
$h_1=h_0+L_f{\tan{\alpha}}$
Wenn der Wert von h₁ größer ist als der Tankdurchmesser, ist ein Teil des Tanks komplett gefüllt mit Flüssigkeit. Dann muss man den völlig gefüllten Teil wie folgt berechnen:
$L_t=\frac{h_1-2{R}}{\tan{\alpha}}$
Die Berechnung des völlig gefüllten Tanks ist sehr einfach, wie man anhand von Zylinder sehen kann.

Nach diesen Berechnungen kann man die teilweise gefüllte Tanklänge $L=L_f-L_t$ und Füllstand h₀ in den Formeln der ersten Sektion ersetzen, um das Volumen eines teilweise gefüllten Teils eines geneigten Tanks zu berechnen.

PLANETCALC 在线计算器

Volumen eines geneigten zylindrischen Tanks

这个页面的存在是由于以下各位的努力:

Anton

Stefan Roesner

Messung des Füllstandes

Flüssigkeitsvolumen in einem geneigten zylindrischen Tanks

Formel für das Volumen eines teilgefüllten geneigten Tanks

Gefüllter Teil der Tanklänge bestimmen

Leerer Teil des Tanks

Voll gefüllter Tank

类似计算器

评论

PLANETCALC 在线计算器

Messung des Füllstandes

Flüssigkeitsvolumen in einem geneigten zylindrischen Tanks

Formel für das Volumen eines teilgefüllten geneigten Tanks

Gefüllter Teil der Tanklänge bestimmen

Leerer Teil des Tanks

Voll gefüllter Tank

类似计算器

评论

分享 本页

分享本页